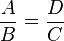cono truncado ;D

En el examen nos vino un problema de cono truncado nos dieron un vaso y teníamos que calcular el volumen de este por eso decidí publicar esto :) 

Volumen de un cono truncado

Área lateral de un cono truncado

Área de un cono truncado

ELSA YEPEZ 4TO "A"

matemática un instrumento para el estudio de la naturaleza .

luego de todo este bimestre, gracias a los proyectos y este blog , fue mas facil entender que las matemáticas no son solamente números y formulas , por ejemplo 

Uno de los aspectos más conocidos de la utilidad práctica de las matemáticas es su gran capacidad para la modelización de fenómenos naturales, ya que el estudio de esos modelos permite entender mejor, explicar, e incluso predecir nuestro comportamiento. Por ejemplo, la estela que deja una barca sobre la superficie de un río puede descubrirse mediante el principio de Huyguens generalizado que se deduce del modelo teórico de propagación de las ondas y su correspondiente ecuación..La descripción de un modelo matemático para la asignación de precio a ciertos tipos de productos financieros les valió el premio Nobel de Economía a Black y Scholes. Curiosamente una de las herramientas matemáticas usada por dichos economistas está directamente relacionada con el modelo de transmisión del calor. Los códigos para las tarjetas de crédito o para la transmisión de mensajes cifrados son aplicaciones directas de la criptografía en la que juegan un papel esencial cuestiones teóricas de las matemáticas llamadas puras. es muy bueno saber esto , ya que nos lleva a tener un cierto interés por el curso  este bimestre aprendimos teoremas que nos llevaron hasta medir longitudes , alturas , la real de una esfera , y al realizar este blog , leímos cosas asombrosas que probablemente muchos no sabíamos .  Maria Del Carmen Lourdes Santos Fernández :B

EL OMNIPOLIEDRO

El Omnipoliedro es una composición realizada con los armazones de los cinco sólidos platónicos de forma que cada uno de ellos está inscrito en del siguiente.

En el interior se encuentra el Octaedro (amarillo), sus vértices se sitúan en el centro de las aristas del Tetraedro (rojo). Los cuatro vértices del tetraedro coinciden con otros tantos del Cubo (verde). Las aristas del cubo se encuentran sobre las caras del Dodecaedro (morado). Y por último, el Icosaedro (azul) proporciona rigidez al Dodecaedro cuando las aristas de ambos se cortan en los puntos medios.

De esta forma conseguimos que resalten tanto las relaciones numéricas (número de caras, aristas y vértices) como las geométricas (planos de simetría, centros y ejes de rotación), que se establecen entre los cinco poliedros.

susana obregón :B

QUE ES PI?

Estaba ordenando mi librero y en eso encontré trabajos de matemática pasados, vi uno que se trataba del valor de la constante denominada PI, me generó mucha curiosidad, así que investigué sobre este todos los datos que pude…

PRIMER DATO:

π (pi) es una constante matemática cuyo valor es el mismo a la proporción que existe entre el perímetro de la circunferencia y la longitud de su diámetro, se usa mayormente en matemática, física e ingeniería .

SEGUNDO DATO

Diversos matemáticos que han participado en el descubrimiento del número “pi” y que habían aportado nuevas cifras; destacan: William Jones, Leonhard Euler, Ludolph van Ceulen, Arquímedes y Euclides.

TERCER DATO:

En la actualidad se han descubierto millones de cifras decimales del número “pi”, y esta cadena de decimales (que parece infinita) continúa…

CUARTO DATO:

Se dice que un japonés fue capaz de estar 16 horas seguidas recitando de memoria cifras del número “pi” sin equivocarse: ¡es increíble lo que puede llegar a conseguir la mente humana! Esos japoneses están cada vez más locos :)

3,1415926535…

susana obregon

PRINCIPIO DE ARQUÍMEDES

"Todo cuerpo sumergido en un fluido experimenta un empuje vertical hacia arriba igual al peso del fluido desalojado"

DATOS QUE PODEMOS CONOCER DEL CUERPO (EN EL VACÍO) ANTES DE SUMERGIRLO

Por medidas directas podemos conocer:

la masa y el volumen 

y a partir de estos datos su densidad: d=m/V .

Conocida la masa se puede hallar el peso en el vacío: p=m·g .

La densidad nos da una idea de como están agrupados los átomos en el cuerpo.

Cuanto más pesados sean los átomos y más juntos estén más denso será el cuerpo.

Si la densidad del cuerpo es igual o mayor que la del líquido el cuerpo quedará totalmente sumergido.

Podemos conocer otras muchas cosas: color, conductividad, tipo de compuesto..., pero no vienen al caso ahora.

¿QUÉ PODEMOS CONOCER DEL LÍQUIDO?

(El P. de Arquímedes se aplica a cualquier fluido aunque aquí vamos a referirnos únicamente a los líquidos).

Por medidas directas:

la masa y el volumen.

Conocida la masa y el volumen podemos conocer la densidad del líquido: d_L=m_L / V

Podemos conocer otras muchas magitudes: viscosidad, tensión superficial, conductividad, composición química etc.

CUERPO SUMERGIDO (Magnitudes que podemos conocer)

Al ir introduciendo el cuerpo en el líquido se va desalojando paulatinamente un volumen de líquido igual al volumen que se va

introduciendo del cuerpo (un volumen sustituye al otro).

El líquido reacciona contra esa intromisión empujando al cuerpo con la misma fuerza que utilizaba para mantener al líquido que estaba allí (en el lugar que ocupa ahora el cuerpo) .

La fuerza empuje es igual al peso del líquido desalojado (el que estaba allí).
El cuerpo se sumerge hasta que el empuje del líquido iguala el peso que tiene el cuerpo en el vacío.

El peso del cuerpo en el vacío (fuerza con que lo atrae la tierra)=masa del cuerpo . gravedad= V_c·d_cuerpo·g

El empuje no depende ni del tamaño del recipiente donde está sumergido el objeto ni de la profundidad a que se encuentre el cuerpo.

Es igual en un lago que en el oceáno, siempre que tengan agua de la misma densidad, y es igual a 20m que a 40 m de profundidad. A grandes profundidades la densidad aumenta y el empuje sería mayor.

Peso del líquido desalojado=masa de líquido desalojado por la gravedad= P_L=m_L·g

Masa de líquido desalojado=volumen de líquido desalojado por la densidad del líquido=m_L=V_L·d_L

El volumen de líquido desalojado es igual al volumen del cuerpo sumergido.

E=V_sumergidod_líquidog

El equilibrio se produce cuando el peso del cuerpo en el vacío=Empuje

Si el peso es mayor que el empuje máximo (cuando está totalmente sumergido), el cuerpo se desplaza hacia el fondo.

Si utilizas unidades del S.I. (metro cúbico, Kg/ m³, 9.8 m/s²), el empuje se obtiene en Newtons.

                                      Mayté Alessandra Palacios Cuya.

TABLA REPORTE 3

MEDICION	LUGAR	D1	D2	D3	D2/D3/D1	REAL
1era	Tablazo	285	915	1200	38,52	38.55
2da	Parque	450	989	1560	34,28	34,32
3era	Garaje	295	214	747	541	545
PROMEDIO					204.6

MARIA FERNANDA GARCIA POMAYA

CRITERIOS DE SEMEJANZA DE TRIÁNGULO

CRITERIO ángulo - ángulo ( A - A )

Si dos ángulos de un triángulo son congruentes a dos ángulos de un segundo triángulo, entonces estos dos triángulos son semejantes.

Es decir , en los triángulos ABC y DEF : ÐA = ÐD   y   Ð B = Ð E

Entonces  ABC ~  DEF

 

CRITERIO lado - ángulo - lado ( L .A .L ) 
 

Dos triángulos son semejantes si tienen dos lados proporcionales y congruentes el ángulo comprendido entre ellos.
Es decir , en los triángulos ABC y DEF ,
Si   Ð A = Ð D  y   AC/DF = AB/DE

Entonces   ABC ~   DEF

CRITERIO lado - lado - lado ( L. L . L . )

Dos triángulos son semejantes si tienen sus tres lados respectivamente proporcionales.

Es decir , en los triángulos ABC y DEF :

Si:

Entonces ABC ~ DEF

Maria isabel cenizario chiri

¿Cuál será la distancia desde la iglesia del pueblo de San Rafael hasta la casa de Román si se hizo la siguiente observación?

Milagros Cuevas

teoerema de tales de mileto

Como hemos estados haciendo experimentos que tienen que ver con el terema de tales entonces decidi darles esta definicion y tambien un problemita para tener claro este tema aqui va :

Si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.

Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?

Sí, porque se cumple el teorema de Thales.

 

Aqui hay una cancion de el teorema de tales escuchenlo :)

http://www.youtube.com/watch?v=czzj2C4wdxY

 Elsa Yepez Westreicher

Tales nos ayudó con el proyecto :)

El otro día en clase de Mate 2 , realizamos un trabajo al aire libre , usamos el teorema de tales para hallar una aproximación a la altura de la escalera 

Si por un triángulo se traza una línea paralela a cualquiera de sus lados, se obtienen dos triángulos semejantes

Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.

Por ejemplo, en la figura se observan dos triángulos que, en virtud del teorema de Tales, son semejantes. Entonces,  entre los lados A y B del triángulo pequeño se iguala a los lados  D y C en el triángulo grande. porque tales nos dice que los triangulos de la figura  son semejantes

asi es como pudimos calcular la medida de la escalera :)

Maricarmen Santos Fernández nº 30 4to A

Un link que pueden visitar :
Taller Geometrico :)
En el cual te enseñan a medir con tan solo un
espejo, una cinta métrica, utilizando triángulos semejantes


Milagros Cuevas

La Fuerza del Triangulo

Si se ejerce una fuerte presión sobre un cuadrilátero se acaba deformando. Lo mismo ocurre con todos los polígonos, excepto el triángulo, que es el único que ofrece una suficiente rigidez. Por eso suele ser utilizado en la construcción de estructuras de gran tamaño que deben soportar grandes pesos, como los andamios. Un buen ejemplo son las torres de tendido eléctrico, que suelen estar hechas de trozos de metal formando una tupida red de triángulos. La torre Eiffel de París, que con sus 300 metros fue durante muchos decenios la construcción más alta del mundo, también esta hecha aprovechando la rigidez del triángulo.

Mili Cuevas :)

Los Astros, la Música y las Matemáticas

Pitágoras y sus seguidores pensaban que las matemáticas gobernaban todas las cosas, incluso los astros. Como además descubrieron la profunda relación entre las matemáticas y la música, creían que los cuerpos celestes se movían regulados por una armonía universal y que esos movimientos producían música. Curiosamente, hace poco que los científicos han descubierto que esta poética interpretación tiene ciertos rasgos reales; el Sol vibra y produce sonidos de diferentes frecuencias que han podido captar las naves Voyager y Ulises porque el viento solar las propaga. El sol emite sus sonidos en frecuencias más graves que los cantantes denominados “bajos”.

Mili Cuevas

¿En qué se parecen un tornillo, una galaxia y un caracol? Todos ellos tienen forma de espiral, una figura geométrica por la que la naturaleza y el hombre parecen sentir especial predilección; las pipas de girasol cuando están en la planta, las telas de las arañas, las caracolas marinas, los cuernos de las cabras, los colmillos del elefante…..El hombre también se aprovecha de sus virtudes y puedes observar que empleamos espirales todos los días, ya que están en los sacacorchos, los ventiladores, los discos musicales, los helicópteros, los rollos de papel, el cable del teléfono o las cintas magnetofónicas. Seguro que si te fijas encuentras más espirales a tu alrededor :)

 Milagros Cuevas

Las abejas saben geometría

Sabemos que las abejas almacenan la miel en estructuras hexagonales, pero  ¿Por qué? si más fácil sería construir triángulos o cuadrados que tienen el mismo perímetro.

 Pappus de Alejandría se dio cuenta que esto no se debía a una coincidencia sino que el área que encierra el hexágono es mayor ya que demostró que  entre todos los polígonos regulares con el mismo perímetro, encierran mas área aquellos que tengan mayor número de lados. Entonces podemos concluir que esta es la forma de almacenar la mayor cantidad de miel ahorrando al máximo la cantidad de cera en las celdillas.

María Isabel Cenizario Chiri  N°: 9

Demostrando el teoremo de pitagoras con geometría

Una propiedad general de las figuras planas semejantes es que sus áreas son proporcionales a los cuadrados de sus correspondientes dimensiones lineales.. Notemos que la hipotenusa de cada uno de los triángulos más pequeños coincide con uno de los lados del triángulo original. Así pues, se sigue al mismo tiempo que el cuadrado de la hipotenusa del triángulo original es realmente la suma de los cuadrados de los otros dos lados: ¡el teorema de Pitágoras!

Llamemos al área del triángulo original y   A1 , A2 a las áreas correspondientes a los triángulos   y . Por tanto,  A=A1 + A2

Pero por las propiedades de las fracciones, si tenemos dos fracciones iguales entonces cada una de ellas es igual a la fracción cuyo numerador es la suma de los numeradores y cuyo denominador es la suma de los denominadores, esto es:

 A1/b2 = A2 / a2 = A1/b2 + A2/b2 = A /a2 + b2

Por otro lado, el triángulo inicial y el triángulo también son semejantes, por lo que cumplen una relación parecida, es decir:

A/c2  = A1 /b2

y al unir la informacion proporcionada por las dos igualdades anteriores obtenemos lo siguiente:

a2 + b2 = c2 , EL TEOREMA DE PITÁGORAS

Maria Del Carmen Santos Fernández nº 30 4to A

Como dichos triángulos son semejantes, tenemos que las proporciones entre el área de cada uno de ellos y el cuadrado de su hipotenusa son iguales, esto es: A1/b2 = A2 / a2