Hola (:
Bienvenido a nuestro Blog :)
AHORA , a aprovechar la info :)
Bienvenidos todos :)
este es nuestro proyecto de Mate 2 , esta hecho para que todos los que ingresen se asombren con curiosidades , juegos matematicos , problemas etc
esperamos que sea de su agrado .
las integrantes de este grupo somos :
Elsa Yepez
Maricarmen Santos
Milagros Cuevas
Maria Isabel Cenizario
Maria Fernanda Garcia
Susana Obregon
este es nuestro proyecto de Mate 2 , esta hecho para que todos los que ingresen se asombren con curiosidades , juegos matematicos , problemas etc
esperamos que sea de su agrado .
las integrantes de este grupo somos :
Elsa Yepez
Maricarmen Santos
Milagros Cuevas
Maria Isabel Cenizario
Maria Fernanda Garcia
Susana Obregon
Mayté Palacios
AHORA , a aprovechar la info :)
Visitaas (:
lunes, 29 de noviembre de 2010
TABLA REPORTE 3
MEDICION | LUGAR | D1 | D2 | D3 | D2/D3/D1 | REAL |
1era | Tablazo | 285 | 915 | 1200 | 38,52 | 38.55 |
2da | Parque | 450 | 989 | 1560 | 34,28 | 34,32 |
3era | Garaje | 295 | 214 | 747 | 541 | 545 |
PROMEDIO | 204.6 | |||||
MARIA FERNANDA GARCIA POMAYA
CRITERIOS DE SEMEJANZA DE TRIÁNGULO
CRITERIO ángulo - ángulo ( A - A )
 Si dos ángulos de un triángulo son congruentes a dos ángulos de un segundo triángulo, entonces estos dos triángulos son semejantes.
Si dos ángulos de un triángulo son congruentes a dos ángulos de un segundo triángulo, entonces estos dos triángulos son semejantes. Es decir , en los triángulos ABC y DEF : ÐA = ÐD y Ð B = Ð E
Entonces ABC ~ DEF
CRITERIO lado - ángulo - lado ( L .A .L )
Dos triángulos son semejantes si tienen dos lados proporcionales y congruentes el ángulo comprendido entre ellos.Es decir , en los triángulos ABC y DEF ,
Si Ð A = Ð D y
Entonces DEF
Dos triángulos son semejantes si tienen sus tres lados respectivamente proporcionales.
Es decir , en los triángulos ABC y DEF :
Si:
Maria isabel cenizario chiri
jueves, 25 de noviembre de 2010
teoerema de tales de mileto
Como hemos estados haciendo experimentos que tienen que ver con el terema de tales entonces decidi darles esta definicion y tambien un problemita para tener claro este tema aqui va :




Aqui hay una cancion de el teorema de tales escuchenlo :)
http://www.youtube.com/watch?v=czzj2C4wdxY
Elsa Yepez Westreicher
Si dos rectas cualesquieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.

Las rectas a, b son paralelas. ¿Podemos afirmar que c es paralela a las rectas a y b?

Sí, porque se cumple el teorema de Thales.
Aqui hay una cancion de el teorema de tales escuchenlo :)
http://www.youtube.com/watch?v=czzj2C4wdxY
Elsa Yepez Westreicher
sábado, 20 de noviembre de 2010
Tales nos ayudó con el proyecto :)
El otro día en clase de Mate 2 , realizamos un trabajo al aire libre , usamos el teorema de tales para hallar una aproximación a la altura de la escalera
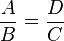
|
Del establecimiento de la existencia de una relación de semejanza entre ambos triángulos se deduce la necesaria proporcionalidad entre sus lados. Ello significa que la razón entre la longitud de dos de ellos en un triángulo se mantiene constante en el otro.
Por ejemplo, en la figura se observan dos triángulos que, en virtud del teorema de Tales, son semejantes. Entonces, entre los lados A y B del triángulo pequeño se iguala a los lados D y C en el triángulo grande. porque tales nos dice que los triangulos de la figura son semejantes
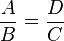
asi es como pudimos calcular la medida de la escalera :)
Maricarmen Santos Fernández nº 30 4to A
lunes, 15 de noviembre de 2010
Un link que pueden visitar :
Taller Geometrico :)
En el cual te enseñan a medir con tan solo un
espejo, una cinta métrica, utilizando triángulos semejantes
Milagros Cuevas
Taller Geometrico :)
En el cual te enseñan a medir con tan solo un
espejo, una cinta métrica, utilizando triángulos semejantes
Milagros Cuevas
jueves, 11 de noviembre de 2010
La Fuerza del Triangulo

Si se ejerce una fuerte presión sobre un cuadrilátero se acaba deformando. Lo mismo ocurre con todos los polígonos, excepto el triángulo, que es el único que ofrece una suficiente rigidez. Por eso suele ser utilizado en la construcción de estructuras de gran tamaño que deben soportar grandes pesos, como los andamios. Un buen ejemplo son las torres de tendido eléctrico, que suelen estar hechas de trozos de metal formando una tupida red de triángulos. La torre Eiffel de París, que con sus 300 metros fue durante muchos decenios la construcción más alta del mundo, también esta hecha aprovechando la rigidez del triángulo.
Mili Cuevas :)
Los Astros, la Música y las Matemáticas

Pitágoras y sus seguidores pensaban que las matemáticas gobernaban todas las cosas, incluso los astros. Como además descubrieron la profunda relación entre las matemáticas y la música, creían que los cuerpos celestes se movían regulados por una armonía universal y que esos movimientos producían música. Curiosamente, hace poco que los científicos han descubierto que esta poética interpretación tiene ciertos rasgos reales; el Sol vibra y produce sonidos de diferentes frecuencias que han podido captar las naves Voyager y Ulises porque el viento solar las propaga. El sol emite sus sonidos en frecuencias más graves que los cantantes denominados “bajos”.
Mili Cuevas
sábado, 6 de noviembre de 2010
¿En qué se parecen un tornillo, una galaxia y un caracol? Todos ellos tienen forma de espiral, una figura geométrica por la que la naturaleza y el hombre parecen sentir especial predilección; las pipas de girasol cuando están en la planta, las telas de las arañas, las caracolas marinas, los cuernos de las cabras, los colmillos del elefante…..El hombre también se aprovecha de sus virtudes y puedes observar que empleamos espirales todos los días, ya que están en los sacacorchos, los ventiladores, los discos musicales, los helicópteros, los rollos de papel, el cable del teléfono o las cintas magnetofónicas. Seguro que si te fijas encuentras más espirales a tu alrededor :)
Milagros Cuevas
martes, 2 de noviembre de 2010
Las abejas saben geometría
Sabemos que las abejas almacenan la miel en estructuras hexagonales, pero ¿Por qué? si más fácil sería construir triángulos o cuadrados que tienen el mismo perímetro.
Pappus de Alejandría se dio cuenta que esto no se debía a una coincidencia sino que el área que encierra el hexágono es mayor ya que demostró que entre todos los polígonos regulares con el mismo perímetro, encierran mas área aquellos que tengan mayor número de lados. Entonces podemos concluir que esta es la forma de almacenar la mayor cantidad de miel ahorrando al máximo la cantidad de cera en las celdillas.
María Isabel Cenizario Chiri N°: 9
Demostrando el teoremo de pitagoras con geometría
Una propiedad general de las figuras planas semejantes es que sus áreas son proporcionales a los cuadrados de sus correspondientes dimensiones lineales.. Notemos que la hipotenusa de cada uno de los triángulos más pequeños coincide con uno de los lados del triángulo original. Así pues, se sigue al mismo tiempo que el cuadrado de la hipotenusa del triángulo original es realmente la suma de los cuadrados de los otros dos lados: ¡el teorema de Pitágoras!
Llamemos A1 , A2 a las áreas correspondientes a los triángulos
Pero por las propiedades de las fracciones, si tenemos dos fracciones iguales entonces cada una de ellas es igual a la fracción cuyo numerador es la suma de los numeradores y cuyo denominador es la suma de los denominadores, esto es:
Por otro lado, el triángulo inicial y el triángulo
A/c2 = A1 /b2
y al unir la informacion proporcionada por las dos igualdades anteriores obtenemos lo siguiente:
a2 + b2 = c2 , EL TEOREMA DE PITÁGORAS
Maria Del Carmen Santos Fernández nº 30 4to A
Maria Del Carmen Santos Fernández nº 30 4to A
Como dichos triángulos son semejantes, tenemos que las proporciones entre el área de cada uno de ellos y el cuadrado de su hipotenusa son iguales, esto es: A1/b2 = A2 / a2
piramides de numeros curiosidad
![[curiosidades+matematicas.jpg]](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEjUPOPIvB_6MpzO0K-4lezTu2BBWTOEQ0wjrKl27YkKJkSq_jTeaJNbPdlwXwo9TfuGClqhsG3hYReWUx4uqo_13CMSMqAawFb8blaMRCmR6fx53Xmzjy3afNM5RPft5jEfDEf5PRiqduqi/s1600/curiosidades+matematicas.jpg)
Se dan cuenta ? lo mismo psa con las piramides con numeros pares observen:

ELSA YEPEZ 4TO "A"
Eureka! Eureka!
Herón II, rey de Siracusa, pidió un día a su pariente Arquímedes (aprox. 287 a.C. - aprox. 212 a.C.), que comprobara si una corona que había encargado a un orfebre local era realmente de oro puro. El rey le pidió también de forma expresa que no dañase la corona.
Arquímedes dio vueltas y vueltas al problema sin saber cómo atacarlo, hasta que un día, al meterse en la bañera para darse un baño, se le ocurrió la solución. Pensó que el agua que se desbordaba tenía que ser igual al volumen de su cuerpo que estaba sumergido. Si medía el agua que rebosaba al meter la corona, conocería el volumen de la misma y a continuación podría compararlo con el volumen de un objeto de oro del mismo peso que la corona. Si los volúmenes no fuesen iguales, sería una prueba de que la corona no era de oro puro.
Arquímedes dio vueltas y vueltas al problema sin saber cómo atacarlo, hasta que un día, al meterse en la bañera para darse un baño, se le ocurrió la solución. Pensó que el agua que se desbordaba tenía que ser igual al volumen de su cuerpo que estaba sumergido. Si medía el agua que rebosaba al meter la corona, conocería el volumen de la misma y a continuación podría compararlo con el volumen de un objeto de oro del mismo peso que la corona. Si los volúmenes no fuesen iguales, sería una prueba de que la corona no era de oro puro.
A consecuencia de la excitación que le produjo su descubrimiento, Arquímedes salió del baño y fue corriendo desnudo como estaba hacia el palacio gritando : "¡Eureka! ¡Eureka! ¡Lo encontré! ¡Lo encontré!".
La palabra griega "¡Eureka!" utilizada por Arquímedes, ha quedado desde entonces como una expresión que indica la realización de un descubrimiento.
Al llevar a la práctica lo descubierto, se comprobó que la corona tenía un volumen mayor que un objeto de oro de su mismo peso. Contenía plata que es un metal menos denso que el oro.
La palabra griega "¡Eureka!" utilizada por Arquímedes, ha quedado desde entonces como una expresión que indica la realización de un descubrimiento.
Al llevar a la práctica lo descubierto, se comprobó que la corona tenía un volumen mayor que un objeto de oro de su mismo peso. Contenía plata que es un metal menos denso que el oro.
SUSANA OBREGON .
Suscribirse a:
Comentarios (Atom)









